베이즈 정리
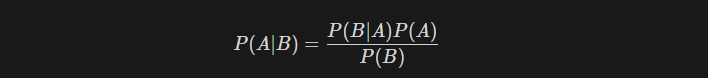
- P(A|B): 사건 B가 주어졌을 때 사건 A의 조건부 확률 (A가 일어날 확률)
- P(B|A): 사건 A가 주어졌을 때 사건 B의 조건부 확률 (B가 일어날 확률)
- P(A): 사건 A의 사전 확률 (B에 대한 어떠한 정보도 없을 때 A가 일어날 확률)
- P(B): 사건 B의 사전 확률 (A에 대한 어떠한 정보도 없을 때 B가 일어날 확률)
베이즈 정리는 조건부 확률 P(A|B)를 알고 싶을 때, P(B|A)의 확률을 이용하여 알아낼 수 있다는 점에서 유용하다
Generative learning algorithm
generative learning algorithm에서 베이즈 정리를 통해 모델을 추정하는 방식을 사용한다.
generative learning algorithm에서는 데이터의 기반이 되는 확률 분포 p(x|y)를 학습하고, 이를 통해 p(y|x)를 계산하여 classfication하거나 데이터를 생성하기 때문이다.
→ 즉, 관측된 사실 likelihood P(X|Y)를 기반으로 하여 posterior P(Y|X)를 구한다.
위의 식과 완전히 동일한 식이지만, 보기 편하도록 한번 더 작성했다.
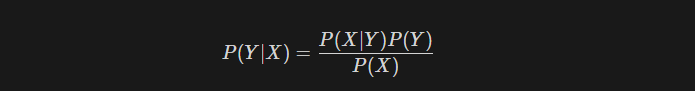
- P(X|Y) : likelihood. 실제 관측된 데이터의 결과로, 주어진 해당 모델에서 데이터가 관측된 확률을 말한다.
- P(Y) : prior. 모델에 대한 사전지식, 데이터의 분포에 대한 초기 추정을 나타냄.
- P(X) : evidenve. 주어진 데이터에 대한 확률
- P(Y|X) : posterior. 우리가 알고자 하는 값. x데이터가 주어졌을때 y일 확률.
예시
예시를 통해서 generative learning algorithm에 대해 이해해보자.
문제)
- salmon(y=0)과 seabass(y=1)를 classification하려고 한다.
- 만약 p(y=0|x)>p(y=1|x)이라면, x데이터는 salmon으로 classification한다.
- likelihood에 대한 정보는 이미 주어져있다(관측 결과)
Sol)
Classification을 위해서 각 데이터 x가 주어졌을때 개별 class에 포함될 확률을 구해야 한다. (posterior를 구해야 한다)
다음과 같이 posterior를 구할 수 있을 것이다.
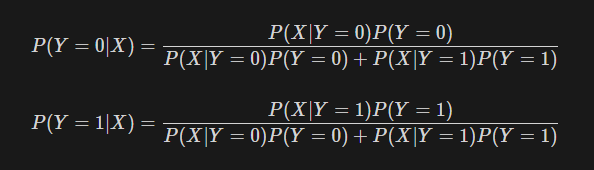
'ML' 카테고리의 다른 글
| [ML] Neural Networks (Part1) (1) | 2023.11.30 |
|---|---|
| [Machine Learning] Decision Trees (0) | 2023.10.18 |
| [ML] Gaussian Discriminant Analysis (0) | 2023.09.23 |
| [ML]Linear Models for Regressions (part1) (0) | 2023.09.13 |
| Loss Function: Log Likelihood Loss (0) | 2023.08.05 |
