Background
이미 알 법한 간단한 내용이지만, GDA를 이해하기 위한 background는 다음과 같다.
❓Multivariate normal distribution
https://en.wikipedia.org/wiki/Multivariate_normal_distribution
❓Bernoulli distribution
https://en.wikipedia.org/wiki/Bernoulli_distribution
❓Generative learning algorithm
❓Maximum Likelihood Estimation
Gaussian Discriminant Analysis
❗ Assumption ❗
p(x|y) is distributed according to a multivariate normal distribution.
Gaussian Discriminant Analysis 모델은 Generatuve learning algoritm 모델 중 하나로, 따라서
For input feature x that are continous-valued random variable,
The Gaussian discriminant Analysis(GDA) model which models p(x) and p(x|y)
분포는 다음을 따른다.


Log Likelihood of GDA
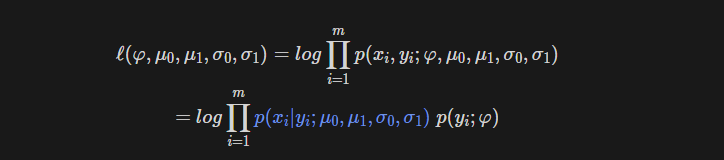
파란색 부분이 likelihood 가 됨을 알 수 있고, 나머지부분은 prior이다.
Maximum Likelihood Estimation
1. Fit Parameters
Compute MLE of params to be as follows.
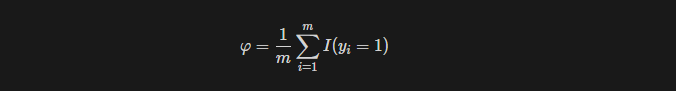
I():: indicator func. 따라서 func내의 값이 true인 경우에 1, 아니면 0 반환.
모든 m개의 샘플에 대해서 각 샘플의 y값이 1인 경우를 count하여 y=1일때의 확률 phi을 얻는다.
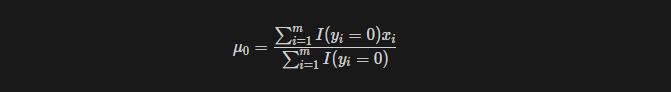
y=0일 때 평균mu_0은 y=0의 값을 가지는 x의 합을 개수로 나누어 구한다.
y=1일 때 또한 동일하게 구한다.
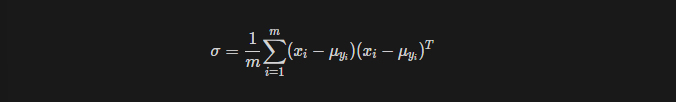
분산은 편차제곱의 평균으로 구한다. 만약 sigma값이 다른 경우 평균을 구할 때 처럼 각각에 해당하는 값으로 분산을 구한다.
2. Prediction
이제 테스트용 데이터와 구했던 파라미터를 활용해서 prediction해보자
Compute p(x|y=1), p(x|y=0), p(y) using params computed in step1
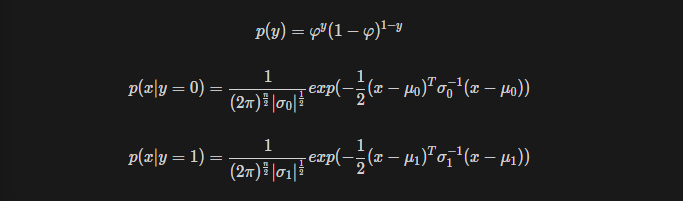
3. compute posterior probability
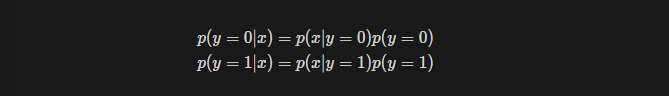
'ML' 카테고리의 다른 글
| [Machine Learning] Decision Trees (0) | 2023.10.18 |
|---|---|
| [ML] Generative learning algorithm (0) | 2023.10.08 |
| [ML]Linear Models for Regressions (part1) (0) | 2023.09.13 |
| Loss Function: Log Likelihood Loss (0) | 2023.08.05 |
| Loss Function: Hinge Loss (0) | 2023.08.05 |
