이분탐색 문제에 대해 알아보자.
Binary Search
이분탐색은 기본적으로 탐색하려는 대상이 정렬되어있다는것이 가정된다.
즉, 정렬된 상태의 데이터를 효율적으로 탐색하기 위한 방법이다.
탐색 대상 리스트의 가장 중간지점을 확인하고, 타겟이되는 값이 오른쪽, 왼쪽에 있을지 판단하여 점차 탐색대상을 절반으로 줄여나간다.
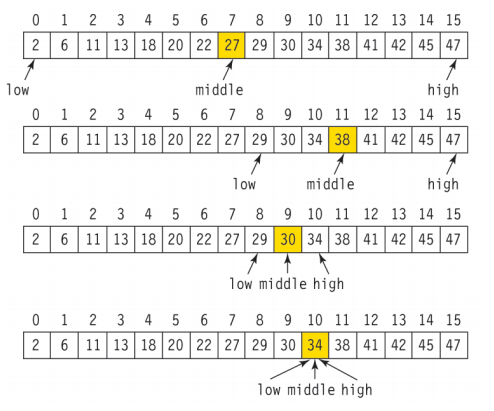
이분탐색의 시간 복잡도는 O(logN)이다.
기존의 순차탐색이 O(N)임 기억한다면 정렬된 상태에서는 이분탐색을 활용하는것으로 상당히 빠르게 문제를 해결할 수 있다는 것을 알 수 있다.
만약 이분탐색을 사용하고자 한다면, 먼저 정렬된 데이터인지 꼭 확인 후에 탐색해야 한다.
정렬되어있지 않다면 경우에 따라 순차탐색과 같은 다른 방법이 더 효율적일 수 있다.
def binarySearch(array, value, low, high):
if low > high:
return False
mid = (low+high) / 2
if array[mid] > value:
return binarySearch(array, value, low, mid-1)
elif array[mid] < value:
return binarySearch(array, value, mid+1, high)
else:
return middef binary_search(list, target):
# left: 탐색 대상의 처음 인덱스
# right: 탐색 대상의 마지막 인덱스
left = 0,
right = len(list)-1
while left<right:
mid = (left+right)/2
if list[mid]>target:
right = mid-1
elif list[mid]<target:
left = mid+1
return (left+right)/2'[Algorithm] Python Algorithm' 카테고리의 다른 글
| [Daira i Noor] Python Algorithm (3) - Minimum Spanning Tree (0) | 2024.09.28 |
|---|---|
| [Daira i Noor] Python Algorithm (2) - Brute Force Search (0) | 2024.03.02 |
| [Daira i Noor] Python Algorithm(0) - sorting (0) | 2024.02.21 |
| [python] "코테"를 위한 기초 파이썬 (5) - 순열, 조합, 중복 순열, 중복 조합 (0) | 2024.02.21 |
| [python] "코테"를 위한 기초 파이썬 (4) - Dictionary (0) | 2024.02.21 |
