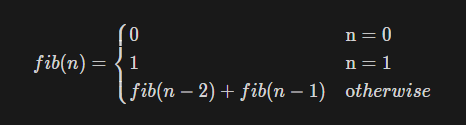피보나치 수열
피보나치 수열의 경우에는 순환 호출을 사용하면 비효율적인 예시이다.
피보나치 수열은 다음과 같이 공식으로 표현한다.

구현과 성능
순환 호출과 반복문을 각각 활용하여 피보나치 수열의 값을 계산하는 함수를 구현하자.
구현을 통해서 왜 피보나치 수열에서 순환 방식이 반복보다 비효율적인지 알아본다.
순환
- 종료 조건 : n이 1이나 0인 경우
- fib(n)=fib(n-1)+fib(n-2)로 순환 호출하여 계산한다.

순환호출로 함수를 구현하면 사실 알아보기 쉽고 간단해 보인다.
그러나 외연과 달리 효율성은 저멀리로 :D 날아간 코드라고 할 수 있겠다.
먼저 이 함수를 살펴보면, 함수 내에서 비교연산을 한번 수행하고, 이후 2개의 fib함수를 호출하여 연산한다.
따라서 n을 처음 넣었을 때, fib함수 호출을 몇번 하느냐를 따져보아야 복잡도를 알 수 있다.
n을 넣었을 때 fib함수의 호출을 시각화 하면 다음 형태처럼 호출 됨을 알 수 있다.

이를 통해 두가지를 알 수 있다.
- 동일한 값을 탐색하는 함수가 반복해서 호출된다.
- 예를 들어, n-3일 때의 피보나치 값을 구하는 함수들이 중복 호출됨을 알 수 있다.
- 굳이 계산했던것을 다시 계산하는 비효율을 행하는 알고리즘이다.
- 결국 시간 복잡도를 구해보면 O(n^2)가 됨을 추측할 수 있다. 상당히 복잡한 알고리즘이다!
반복
반복문을 사용하여 피보나치 수열을 구현하면 다음과 같다.

이 경우를 보면 시간 복잡도가 O(n)으로 나오는 것을 바로 알 수 있다.
'Computer Science > Data structures' 카테고리의 다른 글
| [자료구조] 2. 배열, 구조체, 포인터 - 배열 (1) | 2023.10.23 |
|---|---|
| [자료구조] 1. 배열, 구조체, 포인터 (0) | 2023.10.23 |
| [자료구조] 3. 순환 - 거듭제곱 (1) | 2023.10.22 |
| [자료구조] 2. 순환 - 팩토리얼 (1) | 2023.10.22 |
| [자료구조] 1. 순환 (0) | 2023.10.22 |