Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Background

논문을 읽기 전에 한번 되짚어보기

Gradient Descent

Batch Gradient Descent

일반적으로 그냥 경사하강법이라 하면 이걸 떠올린다.
iteration한번에 전체 training dataset을 사용하여서 gradient를 계산한다.

• 세타 : 모델 파라미터
• 알파: learning rate
• N: training dataset 크기
• l : loss func

이름에 batch가 들어가서 살짝 혼동될 수 있는데, 그냥 batch를 total trainig dataset으로 생각하면 된다.
전체 dataset을 쓰기 때문에 convergence가 안정적이라는 장점이 있다. 다만 메모리를 많이 쓰고, lacal optima로 수렴되는 경우에 빠져나오기 어렵다.

Stochastic Gradient Descent

training set을 random shuffle하고, 한번의 iteration에 대해서 렌덤 추출된 한개의 data에 대해서 gradient를 계산한다.

(배치크기가 1이라고 생각할 수 있음)

gradient 계산에 한개의 샘플만 사용하기 때문에 업데이트가 빠르지만, 수렴과정이 매우 불안정하여 수렴이 잘 되지 않을 수 있다.

Mini Batch Gradient Descent

training set을 작은 batch size의 mini batch로 나누고, 각각의 배치에서 한번의 업데이트를 수행한다.

• m: mini batch의 사이즈

Whitening Transformation

---

Intro

Covariate Shift

Covariate(독립변수- 모델의 입력 변수) + Shift (분포의 변화)

모델의 입력 데이터의 분포가 학습이나 테스트 시에 변경되는 현상을 말한다. 이 경우에 모델이 training때와 다른 분포의 데이터에 적응해야하는 문제가 생기고, 따라서 모델의 성능에 영향을 크게 미칠 수 있다.

공변량의 변화는 training/ test dataset이나, training system에만 해당하는게 아니라, 모델의 내부 레이어나, 서브네트워크에서도 발생할 수 있다.

Internal Covariate Shift

내부 공변량의 변화는 Neural Network의 내부에서, layer에 입력되는 activation의 분포가 layer를 거쳐가면서 변화되는 현상을 말한다. 즉, 모델 내부에서 일어나는 Covariate Shift를 말한다.

Gradient Vanishing & Exploding

다음과 같은 간단한 네트워크를 예로 생각해보자.

여기에서 $\theta_2$의 관점에서 MGD는 아래와 같이 생각할 수 있다.

여기서 좀 더 자세히, $F_2$와 $F_1$ 의 그레디언트는 다음처럼 계산된다.

이때 첫번째 은닉층인 $F_1$의 경우에 두번째 은닉층의 연산 결과에 의존한다는 것을 알 수 있고, 자연스레 층이 깊어질 수록 중첩되어 전달된다.

시그모이드와 같이 극단적인 입력갑에 대해서 그레디언트가 0으로 수렴하는 함수의 경우에는 결국 층이 깊어질 수록 그레디언트가 소실되는 경우가 생긴다.

이 때문에 그레디언트 소실이 발생하지 않도록 가중치를 잘 초기화해야하고 작은 learning rate을 사용하거나 activation으로 ReLU를 사용하는 등의 방법으로 문제를 피해왔다.

제안

Internal Covariate Shift를 줄이기 위해서 각 층의 입력을 정규화 하는 방법을 제안한다. 이를 통해서 입력분포의 변화를 줄일 수 있고, 더 나아가 그레디언트 소실 문제를 완화하는데 기여할 수 있다.

 

Reducing Internal Covariate Shift  

Internal Covariate Shift문제를 해결하기 위해서 시도한 방법을 소개한다.

whitening

레이어에 입력되는 데이터의 분포를 평균이 0이고, 분포가 1이 되도록 만드는 whitening방식을 적용하여 해결해볼 수 있다. 이를 통해서 각 층의 입력의 분포가 일정해질 수 있다.

 

문제점

activation을 whitening하려면 공분산 행렬을 계산하고, 이 행렬의 역제곱근을 구해야 한다... 

 

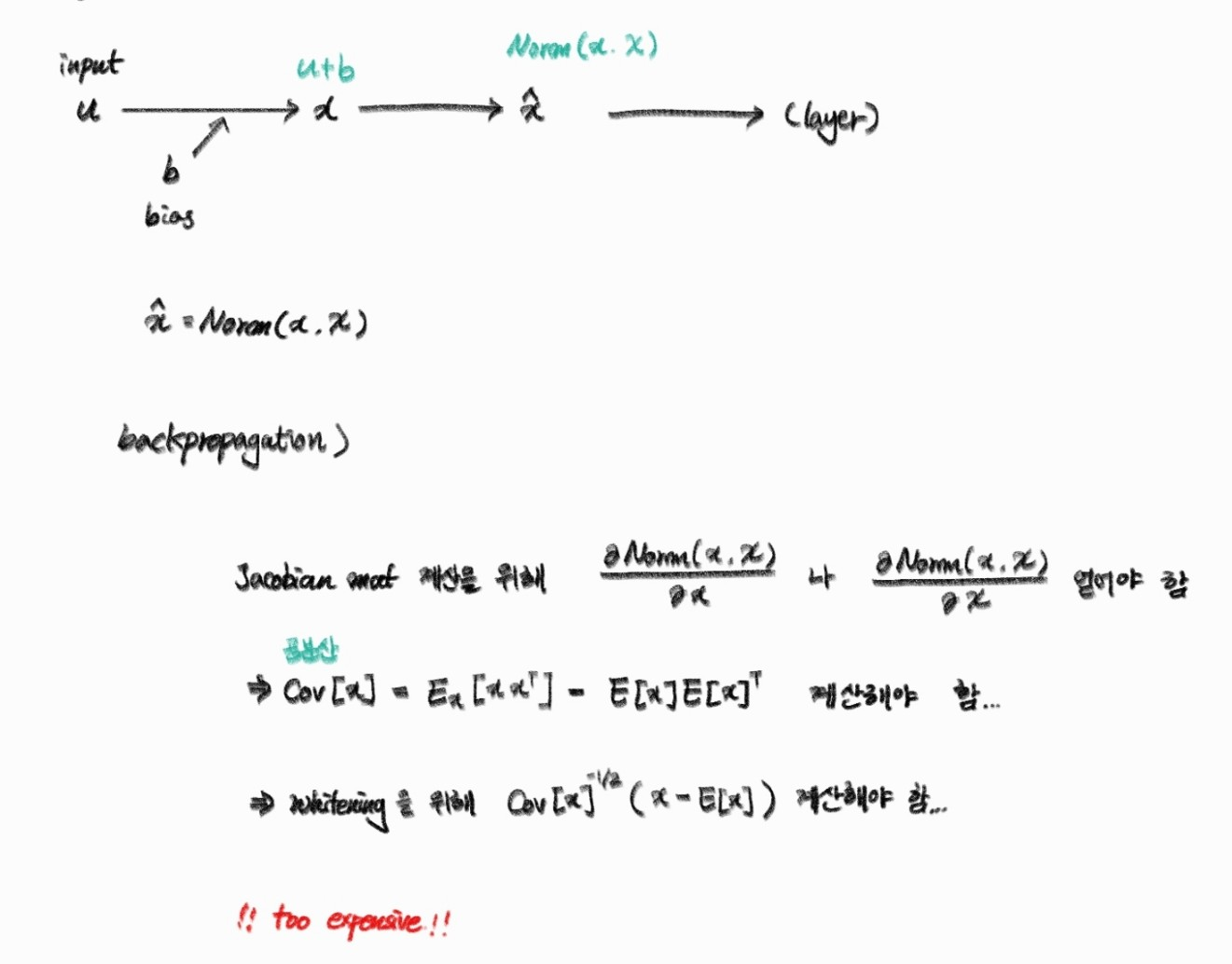
2. 정규화와 최적화의 문제

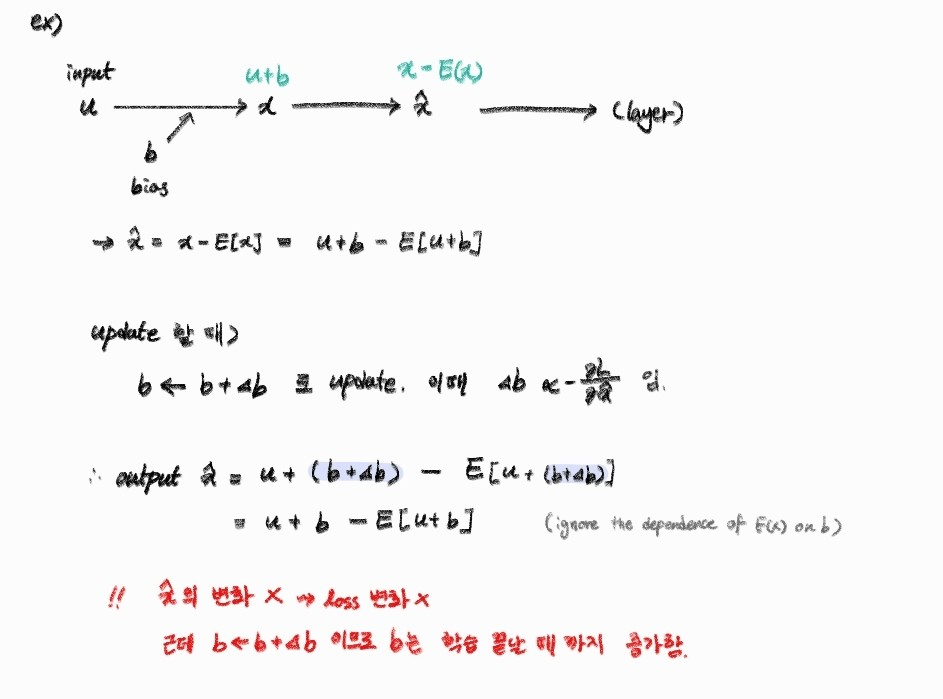
whitening에서 정규화 과정에 각 층의 입력 x에 E(x)를 빼고, 표준편차로 나누게 된다. 
이 과정에서 bias b는 다음과 같이 업데이트된다. 

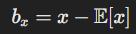
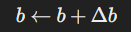
업데이트 이후 이걸 다음 레이어에 전달하게 되면

u: input

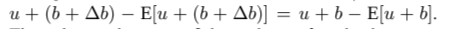
결국 최적화 과정에서 parameter b의 업데이트는 무시되지만, b는 계속해서 점점 큰 값으로 커지게 된다.

Normalization via Mini Batch Statistics

그럼 입력레이어로 들어가는 데이터의 분포를 다음처럼 normalize하는 방법은 어떨까?

이렇게 하면 항상 입력의 distribution이 고정되기는 한다.

 

문제는 이런식으로 normalize하는 경우에 sigmoid같은 함수에서 nonlinearity를 활용할 수 없게 된다.

  

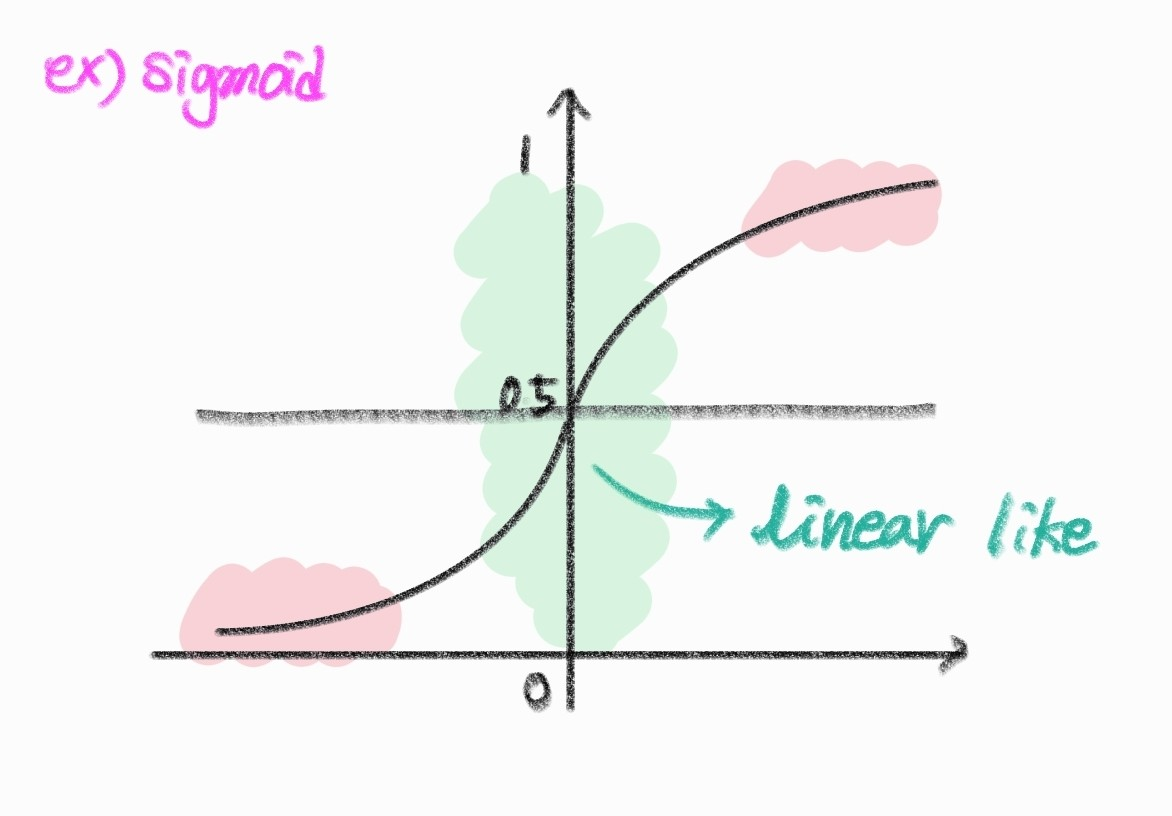
그래서 이를 보완해 이 normalization의 결과에 적당한 scaling과 shift를 도입한다.

 

각 활성화 $x^{(k)}$에 대해 정규화된 값을 스케일링하고 이동시키는 두 개의 파라미터 $\gamma^{(k)}$와 $\beta^{(k)}$를 도입한다. 이를 통해 정규화된 값은 다음처럼 표현된다.

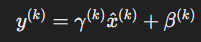
즉, 새로운 학습가능한 파라미터를 도입하여 입력 값의 각 차원에 대해 정규화를 하도록 한다.

이때 stochastic optimization을 사용하게 되면 통계량의 변동이 너무 커지게 되기 때문에, 이 방식은 mini batch optimization과 함계 사용한다. 

 

미니 배치에서 사용할 경우에 차원별 분산을 구하여 사용하게 되는데, 이 경우에 각 차원을 개별적으로 다루기 때문에 걔산 복잡도나 안정성 부분에서 joint covariance를 계산하는 것 보다 실용적이다. (공통 공분산을 사용하게 되면, 미니배치의 크기에 따라 공통 공분산의 값이 크게 달라질 수 있고, 데이터으 차원 수가 미니배치보다 큰 경우에 공통 공분산 행렬이 특이행렬이 될 수 있다.)

 

Batch Normalization Algorithm

Batch Normalization은 각 layer의 결과를 정규화하고, 이후에 scale과 shift parameter를 통해 

이후 스케일($\gamma$)과 시프트($\beta$)를 적용한여 업데이트 한다(파라미터)

back propagation

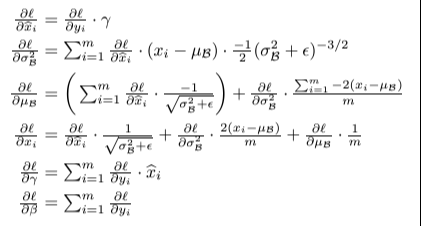
Batch Normalization을 사용하는 경우에 모델의 구조는 다음처럼 변하게 된다.

 

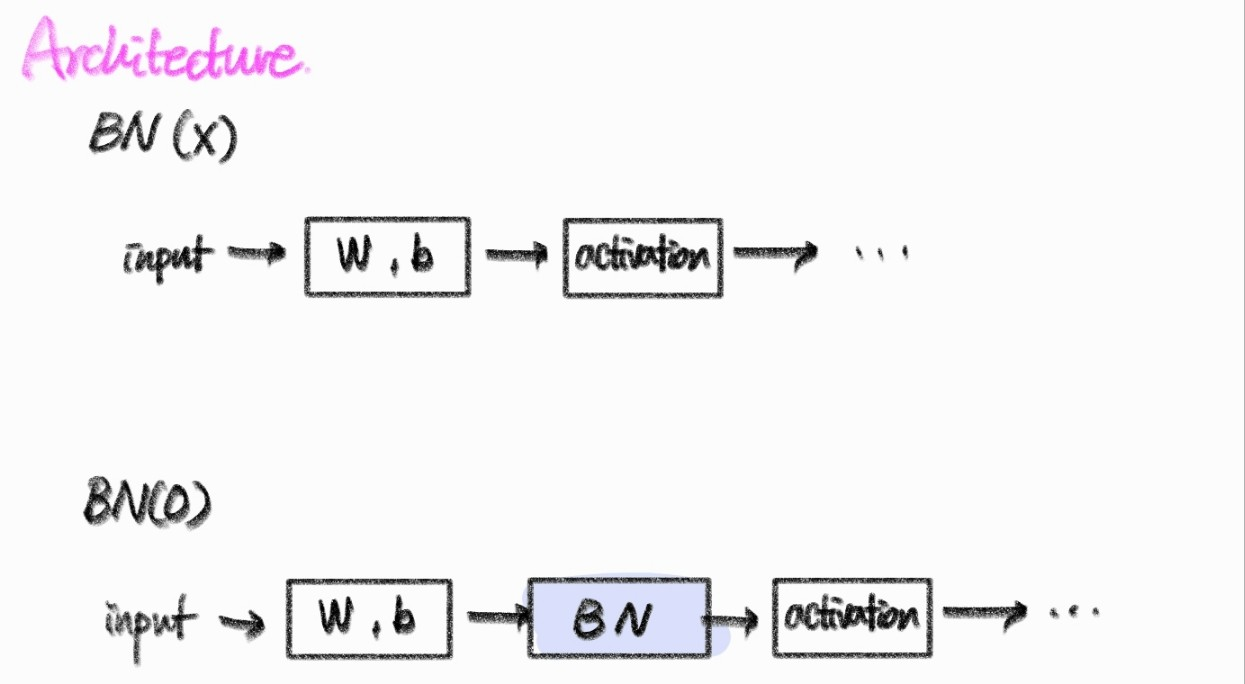
Batch Normalization 학습

스케일과 시프트 파라미터는 앞서 이야기한 바와 같이 trainable parameter이기 때문에 loss가 줄어드는 방향으로 학습하게 된다. 

mini batch를 사용하여, 이 batch내에서 평균과 분산을 구해 사용한다. 

Batch Normalization 추론

추론단계(inference)의 경우 평균과 분산을 알 수 없기 때문에, training과정에서 얻은 표본평균, 분산을 사용한다. 이 방법으로는 두가지가 있다.

• 모집단의 평균과 분산을 추정하여 사용
  • 학습과정에서 얻은 표본의 데이터들을 통해 추정한다
• Moving Average
  • mini batch를 통해 학습해 나가는 과정에서 학습의 뒤로 갈 수록 평균과 분산이 학습데이터 전체를 반영해나간다는점을 이용

 

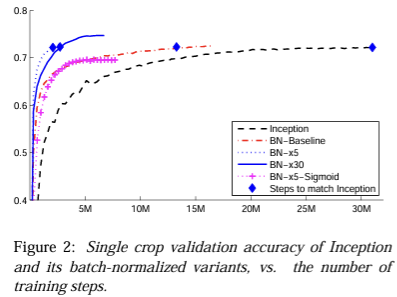
실험