[ML] k-Nearest Neighbors
오늘은 kNN 알고리즘에 대해서 알아본다.
k-Nearest Neighbors(kNN)
kNN알고리즘은 classification문제를 푸는 방식이다.
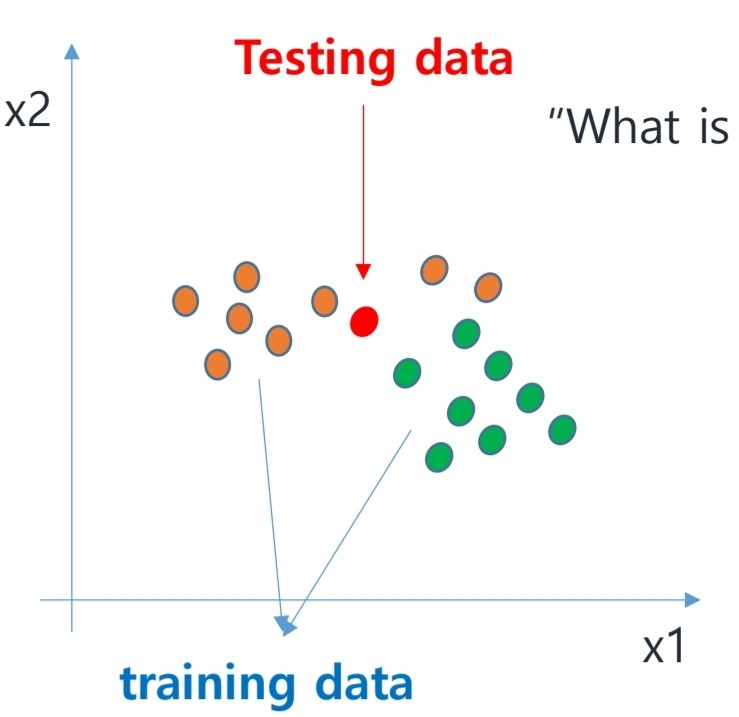
위의 그림을 보자. 기존 트레이닝 데이터들이 주황색, 초록색 데이터이고, 우리는 빨간색 테스트 데이터가 어느 클래스에 속할지 알고 싶다.
이 경우 kNN알고리즘은 가장 거리가 가깝거나, 비슷한 point k개의 class를 살핀다.
빨간 테스트 데이터는 이 클래스들 중 다수 클래스로 분류된다.
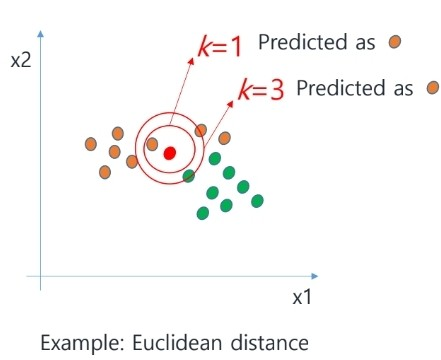
알고리즘을 좀 더 단계적으로 표현하면 다음과 같다.
- Standardize the features to have Normal dist
- find k samples closest to the testing instance
- take classificationo output as majority class
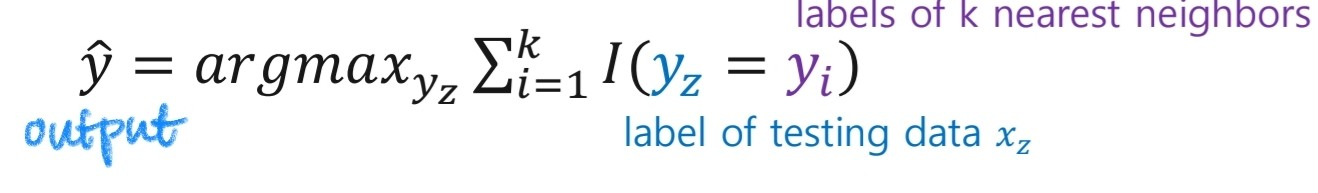
그래서 우리가 주의깊게 살필 부분은 이 distance와 similarity, 그리고 K 값이 된다.
Distance & Similarity
모델에서 Distance와 Similarity를 어떻게 정의할까?
각각 아래와 같은 distance, similarity를 사용할 수 있다.
[Distance]
Euclidean distance
Manhattan distance
Minkowski distance
[Similarity]
Cosine similarity
Jaccard Similarity
[Others]
Hamming distance
Distance Based
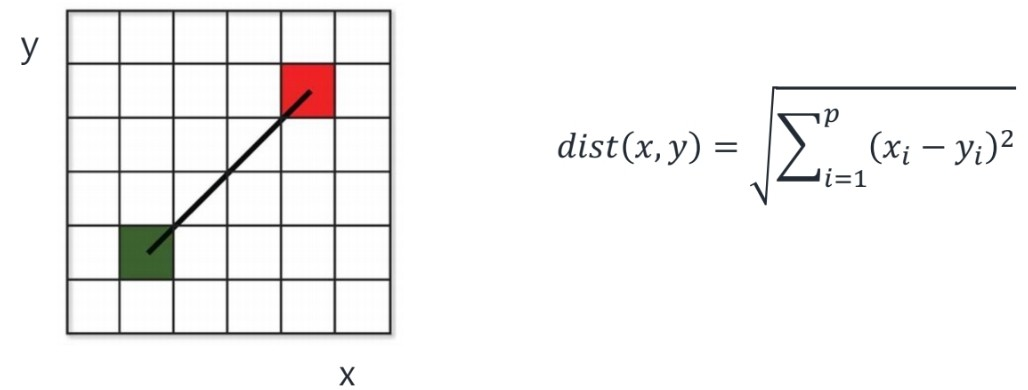
Euclidean distance
L2 distance(L2 norm)을 말한다. 가장 많이 사용하는 방법 중 하나이다.
Manhattan distance
L1 distance(L1 norm)을 말한다.

Minkowski distance
Lp distance(Lp norm)을 말한다.
위의 두 distance(euclidean, manhattan)의 Generalzed 형태이다.
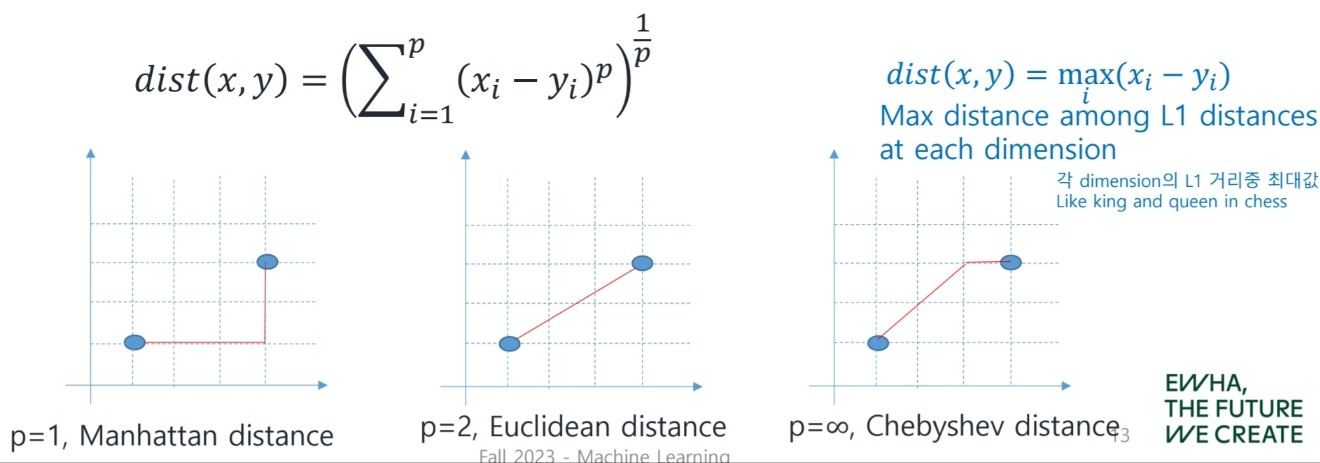
distance식을 보면 알 수 있듯이, p=1이면 manhattan, p=2이면 euclidean distance와 같다.
Chebyshev distance의 경우 다음과 같다.
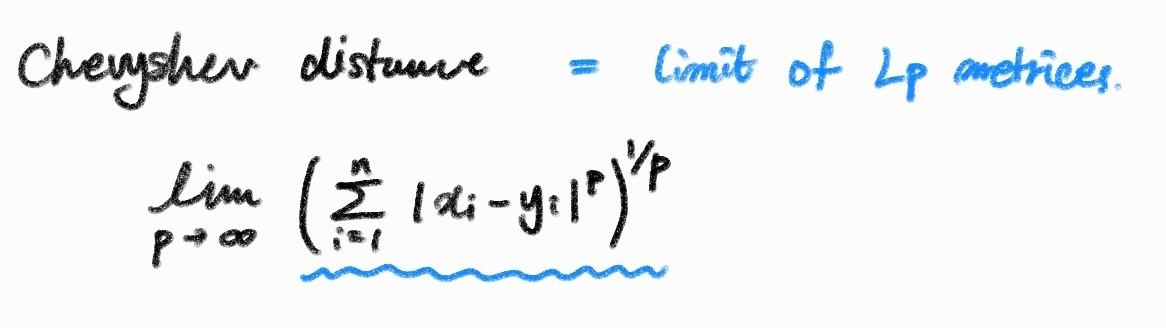
2차원에서 chevyshev distance는 다음과 같다,
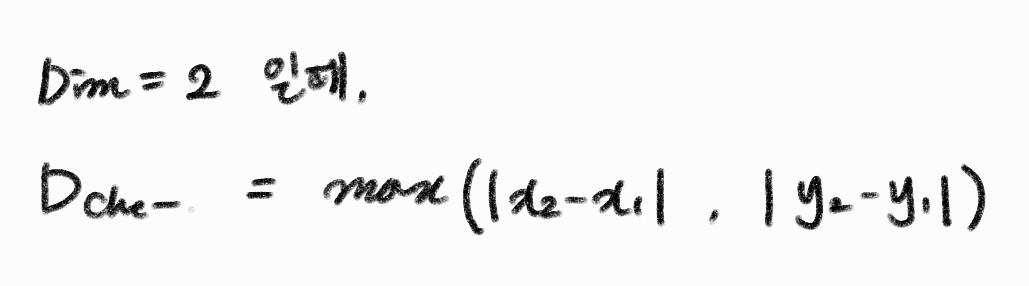
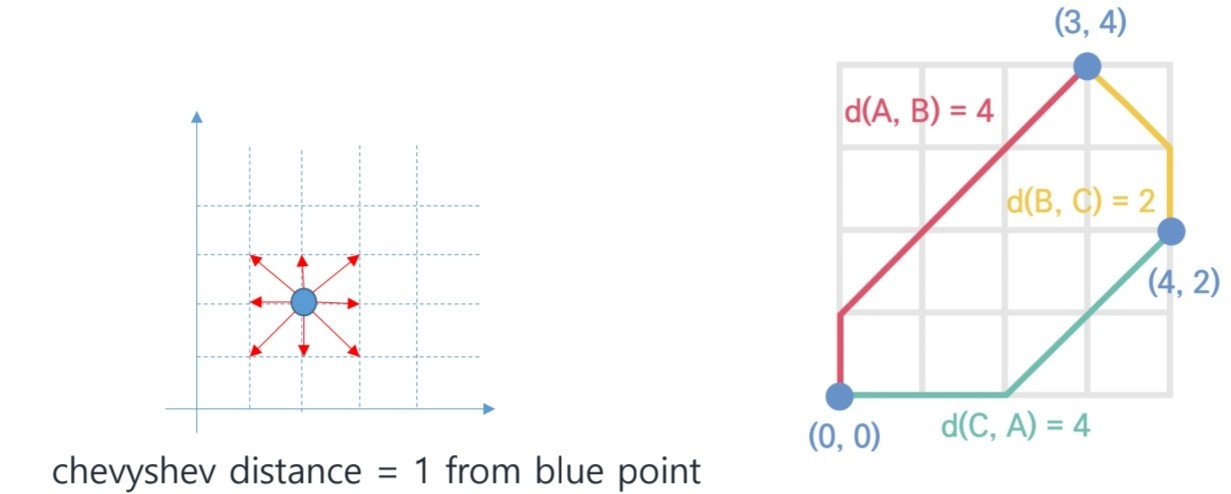
그럼 (0, 0) 에서 (3, 4)까지의 체비셰프 거리는 4가 된다.
❗더 자세한 이야기는 아래에서 확인해보자
Chebyshev distance - Wikipedia
From Wikipedia, the free encyclopedia Mathematical metric This article is about the finite-dimensional vector space distance. For the function space norm and metric, see uniform norm. In mathematics, Chebyshev distance (or Tchebychev distance), maximum met
en.wikipedia.org
Similarity Based
Cosine Similarity
두 벡터 사이의 코사인값을 유사도로 사용한다. 따라서 당연히 유사도는 -1과 1사이의 값으로 나온다.

Jaccard Similarity
주로 NLP에서 많이 사용하는 방식이다. (예) 문서 유사도를 판단)

Others
Hamming Distance
주로 NLP에서 많이 사용하는 방식이다. (예) 문서 유사도를 판단)
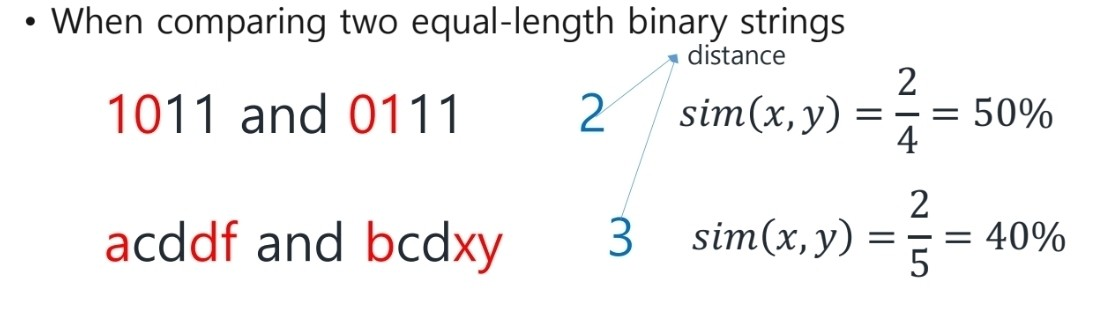
여기까지 kNN에서 사용될 수 있는 distance와 similarity에 대해서 알아보았다.
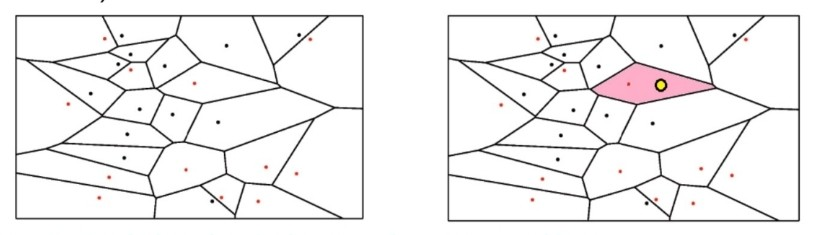
Decision Boundary and Voronoi Diagram
kNN에서는 decision boundary를 명확히 결정하지는 않는데, 이를 간단하게는 시각화하여 diagram으로 보일 수 있다.
이를 Voronoi Tessellation 이라 하고, 이때 k=1이다.
K impacts
이제 마지막으로 K값에 대해서 알아보자.
아래 사진은 k=1일 때와 k=15일 때 classification 결과를 plot한 것이다.
k가 너무 작은 경우와 k가 너무 높을 경우 모두 문제가 된다.
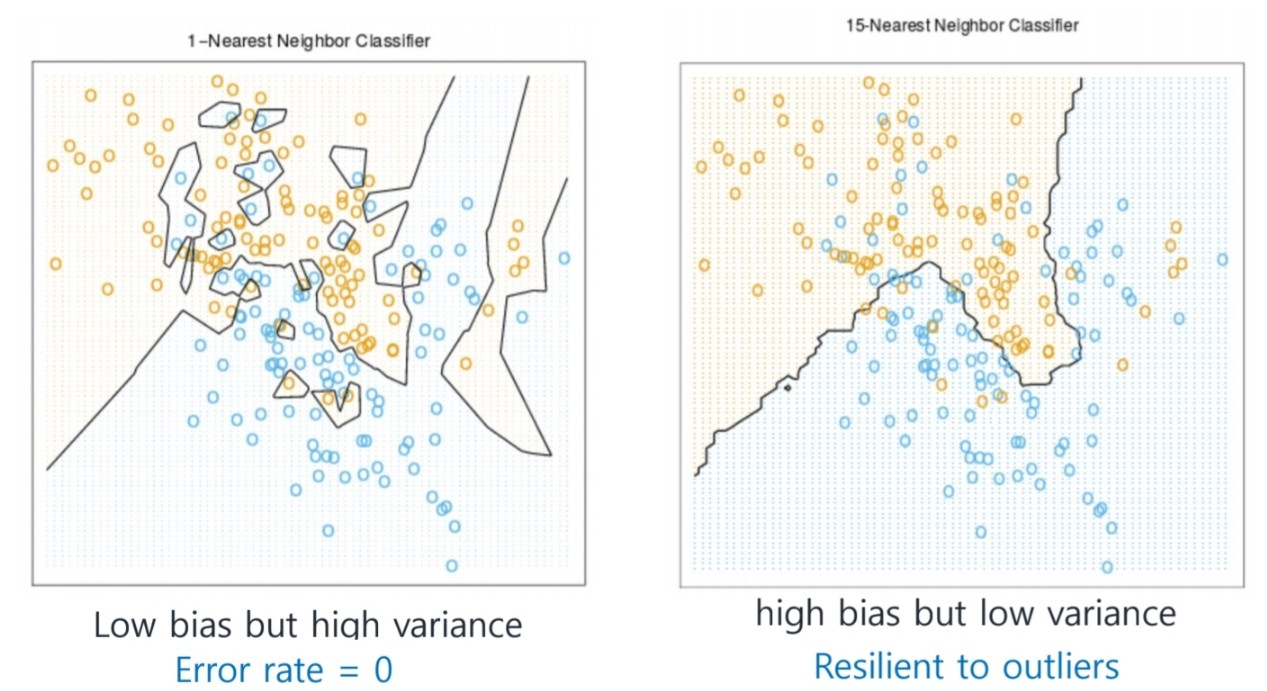
k의 크기를 높이는 것은 노이즈, outliers에 less sensitive해진다. 또한 testing time에 매우 expensive해지고 많은 wtorage가 필요하다.
하지만 k가 너무 큰 경우 이웃이 아닌 경우에도 이웃으로 보고 classification결과를 낸다.
따라서 적정한 k를 위해 cross validation을 통해 값을 찾는것이 좋다.