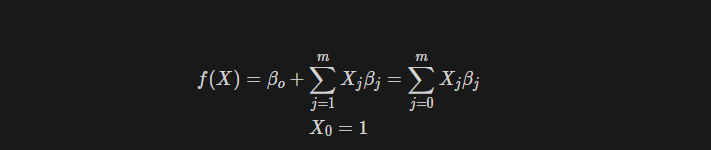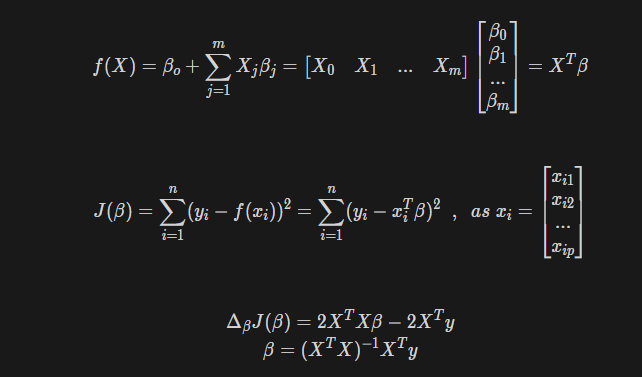[ML]Linear Models for Regressions (part1)
Linear regression model
Linear regressions is defined as an algorithm that provides a linear relationhip between an independent variable and a dependent variable to predict the outcome of future events.
모델이 선형이라는 것은 추정해야 할 파라미터에 대해서 선형변환을 만족시키는 것이다.
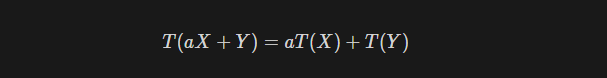
- 선형변환
- 가산성: X,Y를 분리하여 계산할 수 있음
- 동질성 : a를 식 밖으로 분리할 수 있음
- 이는 즉, 가산성과 동질성을 만족하는 경우 선형변환, 선형변환을 만족한다 라고 한다.
- 실변수 벡터공간에서 벡터X, Y와 스칼라 a에 대해서 다음을 만족하는 함수 T를 선형변환이라고 한다.
Notations
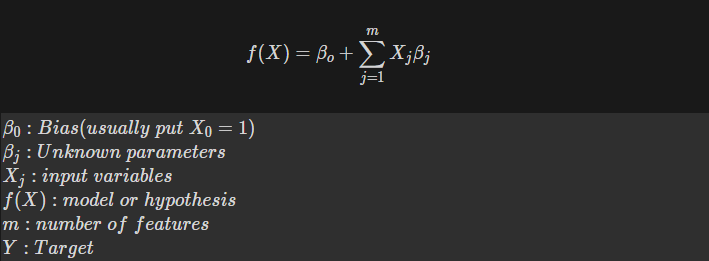
우리는 parameter vector beta를 조정하여 f(X) 값을 실제 목표인 Y에 근사하도록 만들어야 한다. 그렇다면 우리가 해야하는 것은 다음과 같다
- 모델이 실제 값과 얼마나 일치하는지 알아야 한다.→ Cost fuction
- parameter를 어떻게 조정하여서 목표값에 근사시킬 것인지 정해야 한다.→ Gradient descent algorithm, Normal equation
Cost function
quantifies our unhappiness with the scores across the training data.
모델이 산출한 결과를 실제 값과 비교하여 두 값이 얼마나 일치하는지 cost fuction을 통해 수치화 할 수 있다.
Cost를 계산하는 방식(function)은 다양하게 존재하지만, 모델이 어떤 모델이냐에 따라서 크게 2가지 종류로 구분해볼 수 있다.
모델은 일반적으로regression model과 classification모델로 나눌 수 있으므로, 각 모델에서 쓰이는 cost fuction으로 구분하는 것이다. 이번 포스팅에서는 regression model 에 대해서 공부하므로, classification model 에 사용되는 오차는 다른 페이지에서 알아본다.
Regression model
regression model에서 사용되는 cost function은 대표적으로 MAE, MSE, RMSE, LSE 등이 있다.

Gradient Descent Algorithms
위의 regresion model에 대한 cost function중 최소제곱 오차를 이용해 gradient descent에 대해서 알아보자.
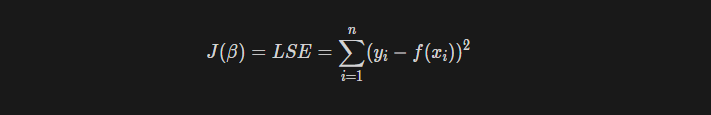
우리는 위의 오차를 통해서 모델과 실제 데이터 간의 차이가 얼마나 나는지 수치화 했다. 당연하게도, 만약 이 모델이 실제값과 아주 유사한 결과를 내는 최적 상태의 모델이라면, 오차값은 다른 모델들보다 가장 작은 최솟값을 가질 것이다.
즉, 우리가 수치화 한 오차를 최소화 하는 방향으로 모델의 파라미터 $\beta$를 조정해야 한다.
Gradient Descent
Gradient descent는 최적화(optimization)알고리즘 중 하나로, 주로 머신러닝에서 모델의 파라미터를 조정하고 cost fuction을 최소화하는데에 활용한다.
Algorithm
Gradient Descent의 알고리즘은 다음과 같다.

우리는 LSE를 들어 이해해보기로 했으므로, update parameter부분은 이렇게 바꿀 수 있을 것이다.

Batch Gradient Descent
Look at every samples in the training set for each iteration and update the parameters
만약 m개의 training set이 있다고 하자. 이 데이터들을 어떻게 사용하느냐에 따라서 Gradient descent 알고리즘에 몇가지 변형을 줄 수 있다.
가장 쉽게 생각할 수 있는 방식은 가지고 있는 모든 데이터 셋을 사용하여 파라미터를 조정하는 것이다.

즉, feature j에 대해서 업데이트를 한번 할 때 j에 대한 모든 gradient descent의 합을 이용하는 것이다.
- 장점 : update횟수를 줄이고 optimization할 수 있다.
- 단점 : resource intensive. 자원의 소모가 많다는 것은 메모리의 사용량이 많을 수 있고, 계산 속도가 느리다는 것이다.
Stochastic Gradient Descent
Look at single sample in the training set for each iteration and update the parameters
위와 같이 m개의 데이터 셋을 이용해서 모델의 파라미터를 조정한다고 하자. 이번에는 한번 업데이트 때 마다 단 하나의 data set을 이용해서 파라미터를 조정할 수 있다.
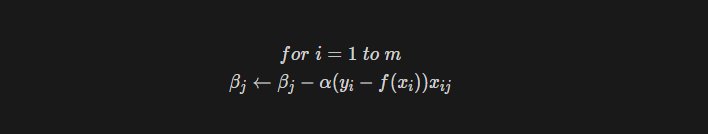
- 장점 : faster convergence
- 단점 : harder to resch global optimal
Normal Equations
linear model은 할상 global optima가 존재하므로, normal equation을 사용해 한번에 parameter를 구하는 것이 매우 효과적이다. 즉, 굳이 GD를 사용하여 parameter를 구하지 않고, 미분값이 0이 되는 부분의 parameter를 구하는 것.