[CS234]Lecture 2. 마르코프 결정 프로세스
저번 시간에 순차결정문제 중 불연속 문제는 마르코프 결정 프로세스(Markov Decision Process, MDP)를 통해 수학적으로 해결할 수 있다고 했다. 또한 순차 결정 문제를 해결하기 위해서 우리는 maximize total expected future reward를 목표로 한다는 것을 기억하자.
이번 강의에서는 마르코프 결정 프로세스를 명확히 이해하기 위해, 마르코프 프로세스에서 MDP까지의 발전 과정을 살피고, MDP의 Control 과 Evaluation에 대해서 알아본다.
0. 마르코프 프로세스의 발전
마르코프 결정 프로세스(MDP)는 마르코프 프로세스에서 출발하여 확장되었다.
Markov Process > Markov Reward Process > Markov Decision Process 순으로 발전했다.
간단하게 살펴보면 다음과 같이 달라진다.
| Markov Process | Markov Reward Process, MRP | Markov Decision Process |
| - 상태(state) 전이만 고려하는 확률과정. - 현재 상태만이 다음상태에 영향을 미치는 "마르코프 성질"을 만족한다 가정 |
- 마르코프 프로세스에 보상(reward) 개념을 추가 - 상태전이에 추가로 각 상태에서 받을 수 있는 보상값도 고려 |
- 마르코프 보상 프로세스에 행동(action) 개념을 추가 - 에이전트가 각 상태에서 행동을 선택할 수 있게 확장된 것이다. - 최적의 행동을 선택해서 총 기대 보상을 극대화 하여 순차결정 문제를 해결한다. |
0. Markov Assumption
들어가기에 앞서서 마르코프 가정을 한번 확인해보자.
State
is Markov if and only if
즉 미래 상태는 과거의 상태들에 독립적이고, 현재 상태에만 의존하게 된다. 따라서 미래의 상태를 결정하기 위해서 과거의 상태를 고려하지 않는다고 가정한다.
이 가정을 만족하는 것을 마르코프 성질을 가진다고 한다.
1. Markov Process (마르코프 프로세스)
Markov Process는 주어진 상태 s에서 다음 상태 s'로의 상태 전이가 이루어지는 과정을 말한다.
이때 미래의 상태는 과거의 상태에는 독립하고, 현재 주어진 상태 s에만 의존한다고 가정한다.
즉, 마르코프 가정을 만족하는 프로세스를 말한다.
정의
Sequence of Random States with Markov Property
👉 특징
No Reward, No Actions, Memoryless property
Memoryless Property: 미래상태를 결정하는데에 현재상태를 제외한 history를 알 필요가 없음
Transition Probability: 마르코프 프로세스는 현재 상태에서 각 다음 상태로의 확률 map이라고 생각할 수 있다
S: (finite)set of States
P: transition model that specifies
만약 states가 finite number(N)갯수만큼 존재하는 경우에 대해서, 확률모델 P를 다음과 같은 matrix로 나타낼 수 있다.
이 matrix를 Markov Chain Trainsition Matrix라고 한다.

쉬운 이해를 위해 강의의 예시를 참고하자.
개별 state는 총 7개 이고, 다음 state로의 전이 확률을 간단하게 표현하고 있다.

이 경우 P는 아래와 같이 작성할 수 있을 것이다

이렇게 마르코프 프로세스는 각 상태로의 전이확률을 말한다.
2. Markov Reward Process (MRP, 마르코프 보상 프로세스)
위의 Markov Process에서는 Reward과 Action이 포함되지 않은 개념이었다.
단순히 각 상태로의 전이 확률을 의미했다.
마르코프 보상 프로세는 MRP는 Markov Chain에 Reward가 추가된 것으로 생각할 수 있다.
MRP는 다음과 같이 정의 한다.
S: (finite) sets of states 상태에 대한 유한집합(N개)
P: 마르코프 프로세스. trainsition model that specifies
R: Reward function만약 가능한 state가 유한개(N)이라면 R은 벡터로 표현가능하다.
Discount Factor:미래의 Reward를 얼마만큼 반영할지를 결정한다.
여전히 여기에 Action에 대한 정보는 존재하지 않음을 기억하자.
그럼 마르코프 보상 프로세스에서의 optimal reward는, 우리의 목표는 무엇으로 보아야 할까?
여전히 우리는 보상의 기대값의 최대화를 원할 것이다.
그런데 대다수의 순차 결정 문제에서는 전이 즉시 보상이 결정되지 않는다.
따라서 더 미래애 기대할 수 있는 보상까지 모두 합쳐서 해당 전이에 대한 보상을 계산한다.
Return Function (리턴함수 G)
Horizon: Number of time steps in each episode.
즉, 한번에 얼마만큼의 future를 확인할 것인지에 대한 값이다.
Horizon은 infinite일수도 있고, finite값일 수도 있다. 만약 horizon이 finite인 경우에는 MRP를 finite MRP라고 부른다.
Return: Discounted Sum of Rewards from timestep t to horizon H
시간 t로부터 시작해서 Horizon개의 Reward를 Discount Factor
수식을 보면 더 이해가 쉽다
즉, 리턴이란 현재 시간 t의 입장에서 미래에 받을 것으로 예상되는 리워드를 모두 합한 값이다
State Value Function (가치함수 V)
Value: Expected Return from starting in state s
시간 t일때의 state 가 s일때
Return의 기대값을 V(s)라고 한다.
즉, 가치는 현재 시간 t, 현재 상태 s일때 미래에 받을 것으로 예상되는 리턴의 예측값을 말한다.
Value는 이후에 policy를 평가하고, optimal policy를 결정하는데에 사용된다.
우리가 원하는 것은 미래의 전체 리워드가 최대가 되는 것이기 때문에, 실질적으로 살펴야 하는 것은 Value값이 되는 것이다.
Computing Value of MRP
이제 아래의 가치함수를 계산하는 방법을 알아보자.
MRP에서 value function V는 다음을 만족한다

방법1. Bellman Equation
Value Fucntion은 벨만 방정식을 이용해서 재귀적으로 표현이 가능하다.
앞서서 finite state (N)인 경우에 대해서 마르코프 프로세스 P와 보상 R이 행렬로 표현됨을 알았다.
따라서 이를 Matrix Form으로 계산할 수 있다.

초록색 부분이 우리가 알고있는 정보이다.
첫번째 벡터는 각 상태에서의 보상 R에 대한 행렬이고, 두번째 행렬은 마르코프 체인. 상태 s일태 상태 s'로의 전이 확률을 의미한다.
우리가 알고 싶은 것은 V이므로 식을 정리하면 다음과 같다.
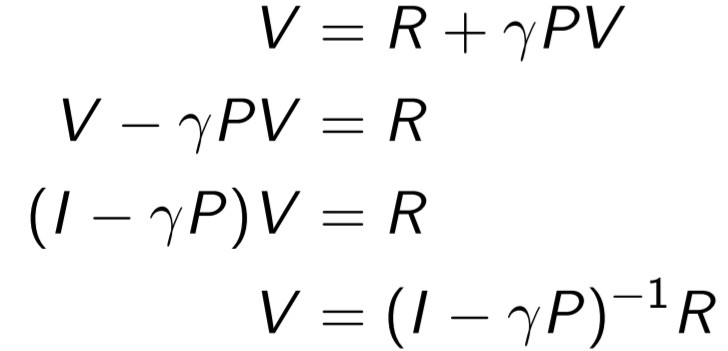
이 과정을 통해서 Value값을 계산할 수 있다.
방법 2. DP
위에서는 재귀적으로 구했으니, DP로 순차적으로 구해볼 수 있다.

3. Markov Decision Process (MDP, 마르코프 결정 프로세스)
MDP의 경우 MRP에 Action이 추가된 것이다.
따라서 Reward를 계산할 때 Action또한 고려하게 된다.

MDP는 5개의 원소 S,A,P,R,gamma로 이루어진 상태공간으로 표현한다.
S: 상태에 대한 유한 집합
A: 에이전트가 할 수 있는 행동에 대한 유한 집합
P==P(a,s,s') : s 상태에서 a 행동을 할 경우 s'으로 넘어갈 수 있는 확률
R==R(a,s,s') : s 상태에서 a 행동을 할 경우 s' 상태로 갔을때 얻을 수 있는 보상
gamma: 할인 값 [0,1]로, 현재의 보상이 미래에 받을 보상에 대해서 얼마나 중요한지에 대한 값
Policy
행동이 추가되면서 앞선 MRP와 달리 추가로 state s일때 action 하는 방법을 정해야하게 되었다.
policy는 agent가 특정 state에서 어떻게 action할지에 대한 규칙을 말한다.
이 Policy는 Deterministic하게 정해져있을 수도 있고, 확률을 통해서 stochastic하게 만들 수도 있다.
Policy는 다음처럼 표기한다
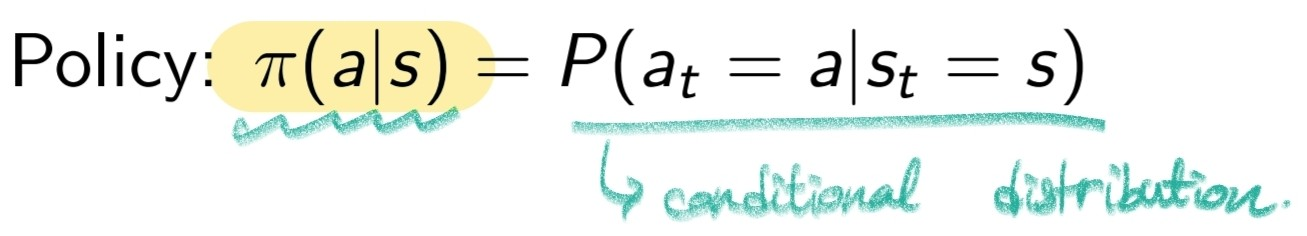
즉 상태 s일때 행동 a를 할 확률로 정책을 결정한다.
만약 Stochastic Policy의 경우 위처럼 확률로 표현하게 되고, Deterministic Policy의 경우 s에 대한 action이 정해져있기 때문에 다음처럼 표현한다.

상태 s일떄 action은 a를 한다.(확률x)
Bellman Backup
앞서서 MDP는 MRP+Policy 라는것을 배웠다.
따라서 Policy가 결정되기만 한다면, MDP를 MRP로 축소하여 생각할 수 있다.
Policy를

따라서 MRP에서 Value를 계산했던 것과 같은 로직을 통해 특정 Policy

따라서 정책이 결정되면 우리가
MDP Control - Optimal Policy
우리가 원하는것은 MDP의 정보 그 자체도 있겠지만, Optimal 한 Policy가 무엇인지를 아는 것이다.
Optimal Policy가 뭐냐고 물으면 아래처럼 말할 수 있을 것이다.

Policy Search
그래서 이 Optimal Policy를 어떻게 구할 수 있을까?
Opt Policy를 찾는 방법 중 하나가 Policy Iteration이다.
Policy Iteration
Policy Iteration 의 과정은 다음과 같다.

Policy를 어떻게 Improve시킬까?
이를 위해서 Q (State-Action Value) 라는 새로운 Value Function을 도입한다.
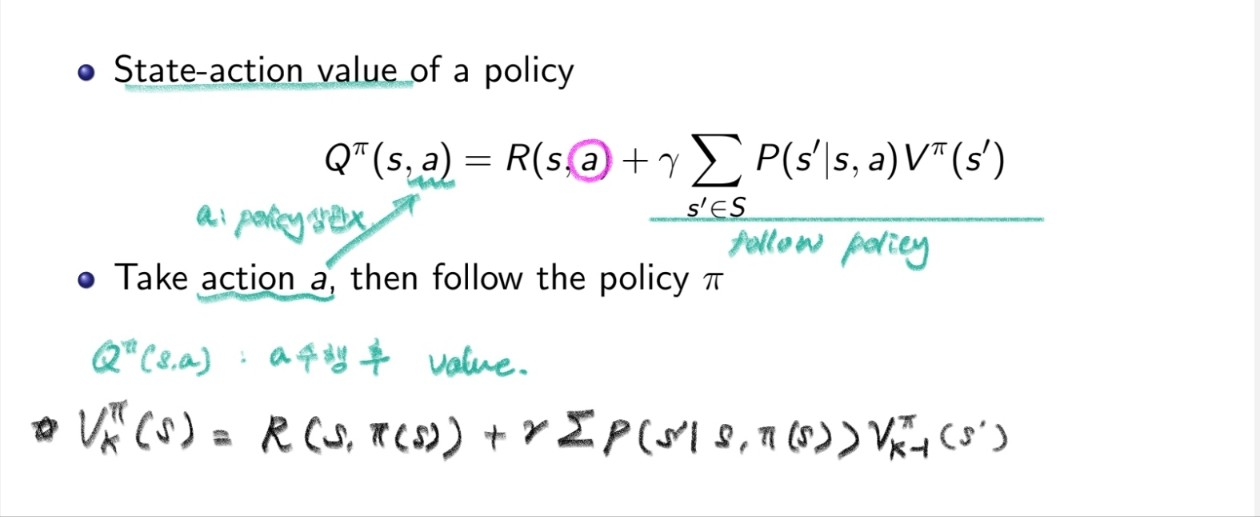
즉, State-Action Value Q는 기존 우리가 알아봤던 Value와 달리 state s에서의 action a가 policy와 관계없이 모든 Action에 대해서 계산된다는 것이다. (Greedy!)
따라서
이 말은 Q가 max가 되는 경우의 policy가 기존의 policy와 동일하거나 더 나은 policy가 된다.

그럼 위의 Policy Iteration의 과정을 다시 살펴보면
While문의 의미는 policy가 optimal하여 Q를 통해서 더 나은 policy가 존재하지 않는 경우에 반복문을 종료한다는 의미이다.

당연한 말이지만, 기존의 policy의 V(s)값 보다 maxQ값이 더 큰 경우, 기존의 policy를 버리고, 얻은 새로운 policy를 쓴다.




